A-Level Physics Required Practicals:
Investigating Diffraction Using a Laser

Many teachers are – quite rightly – concerned about the safety implications of using multiple lasers in a class, even with reasonably sensible students. Particular concerns include:

• With multiple sets of apparatus it can be hard to avoid having laser beams (or their reflections or diffraction paths) criss-crossing the lab.
• In many labs it’s hard to achieve a good blackout, and that carries its own classroom management issues: do you have appropriate places to store coats and bags, for example? What about trailing cables and other trip hazards, in a darkened environment?
• Lasers can be sourced for very little money, but they’re often more powerful than the claimed “<1 mW”. Christina started what turned out to be an interesting discussion about how one might check this, on Talk Physics (registration required).

As ever, one should check with CLEAPSS. Here’s their guidance on lasers (PDF link). Their recommendation is to purchase from an established office or IT supplier, and to ensure the specific unit you receive has a CE marking and a classification BS EN 60825 Class 2. But that’s a summary: read the CLEAPSS advice in full.

It is possible to avoid lasers by using a white light source with a coloured filter. However, to get good results the source needs to be very bright, ideally narrow (collimated), and as close to monochromatic as possible. In practice the filter often costs more than a suitable laser, but if you’d like to explore the option, here’s a write-up at Practical Physics.

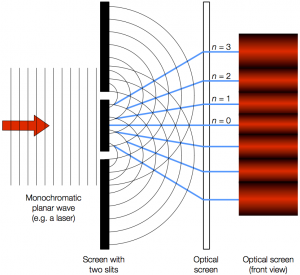As shown in the film, different exam boards and textbooks use different notation for the formula governing the diffraction of light using a double slit aperture:

\(\lambda = ax / D\)

where:

• \(\lambda\) = wavelength of light (to be found)
• \(a\) = slit spacing, between centres – this information is probably printed on a double-slit slide.
• \(x\) = fringe separation, between adjacent maxima or minima. Measure with a ruler or Vernier callipers, or use mm squares on graph paper as the screen.
• \(D\) = distance from slits to screen, which should be as large as possible (ideally 2 m or more).

Alternatively:

\(\lambda = ws/D\)

where:

• \(s\) = slit spacing
• \(w\) = fringe separation

A straightforward calculation can be done, or you can use the graphical method Alom describes in the film at 1’04”, plotting the fringe separation obtained for a range of different \(D\) values and using the gradient to calculate \(\lambda\). You can check the value you obtain against the value stated on the laser and see if it agrees, within your experimental uncertainty.

Questions you might ask your students:

• Why is a laser a particularly suitable light source for this experiment?
• What would happen to the fringe spacing if we used a green or blue laser? Why?
• Why do we want \(a\) (or \(s\)) to be as small as possible, and \(D\) as large as possible?
• What are the uncertainties in the measured quantities, and how do we combine those to arrive at an uncertainty in \(\lambda\)?

Diagram

We have a PDF version of the above diagram available for download.

This is an alternative or additional method. The pattern obtained is easier to see, since the bright fringes (maxima) are well-defined ‘spots’. however, the mathematics involved is a little more involved, and students must use trigonometry to find the diffraction angle \(\theta\).

In the film, Christina sets up the apparatus vertically, which both requires less space in the lab and reduces concerns over laser safety. However, you will still need to be cautious for stray reflections.

The relationship here is

\(n\lambda = d \sin\theta\)

where:

• \(n\) = the order of the maximum, with \(n=0\) as the central maximum, \(n=1\) for the ‘first order’ to either side, and so on.
• \(\lambda\) = wavelength of light
• \(d\) = slit spacing. Usually a diffraction grating slide states the number of lines per mm. For example: 300 lines/mm implies 300,000 slits/m, so \(d = 1/300,000~\mathrm{m}\).
• \(\theta\) = angle between the straight-through direction (helpfully marked by the zero-order maximum) and the maximum being investigated. This must be found using trigonometry:

As stated in the film (at 3’15”), we cannot use the small angle approximation here, since the angles are too large. Hence:

Using the measurements in the film, Alom’s miraculous ‘off-the-cuff’ calculation went like this:

• Total distance = 191 mm, so \(x\) = 191/2.
• \(D\) = 225 mm
• So \(\theta = \tan^{-1}((191/2)/225) = 22.9985\) ≈ 23.0°

Now, to calculate the wavelength:

\(n\lambda = d\sin\theta\) or \(\lambda = \frac{d\sin\theta}{n}\)

Since we measured two fringes either side of the central maximum (for accuracy):

• \(n = 1\)
• \(d = \frac{1}{300,000}~\mathrm{m}\)
• \(\lambda = (\frac{1}{300,000}\sin 22.9985)/2 = 6.5118 \times 10^{-7} = 651~\mathrm{nm}\) (to 3 sf).

Again, students can compare this with the manufacturer’s stated value; the students should be able to assess their uncertainty to check that the manufacturer’s value falls within their uncertainty range. The same discussions as above can be had about how to minimise uncertainties, and what would happen if a different colour laser were to be used.

Christina suggests in the film that for an extension activity, students could be given an unmarked diffraction grating with a different (and unknown) slit spacing, and asked to use the laser wavelength they’ve calculated to measure the slit spacing. As set out earlier, white light could be used with a colour filter, and the comparisons of uncertainties would be interesting.